KTUG마당은 KTUG를 방문하는 모든 이용자가 대화를 나누고 소식을 전하는 곳입니다.
- 로그인 없이 자유롭게 글을 읽고 쓸 수 있는 철학은 처음과 같이 계속됩니다.
- Team Blog의 글을 이곳 게시판의 "정보글"로 모았습니다. Team blog는 기고자가 올린 글에 질문을 받는 부담을 줄이기 위하여 댓글을 허용하지 않았습니다. 그러나 이곳 게시판으로 모으면서 댓글을 달 수 있습니다. 게시물을 작성하실 때 댓글을 원하지 않으시면 댓글을 허용하시지 않으시기를 바랍니다. 또한 불필요한 소모성 댓글을 달지 않도록 주의하여 주시기를 바랍니다.
- TeX과 관련된 질문이나 답변은 QnA 마당을 이용하십시오. TeX과 관련된 질문은 지웁니다
- MathJax를 이용한 수식조판을 사용하실 수 있습니다. 여기를 참조하세요.
- 스팸 글을 막기 위하여 짧은 시간 내에 다시 글이 등록되는 IP를 막거나, 광고 글을 막기 위하여 금지어로 .com, .net 등을 설정하고 있습니다. 다소간의 불편함이 있으시더라도 양해 바랍니다.
- 금지어에서 stackexchange, stackoverflow, ctan, overleaf, , github, google.com, gmail.com, .org, .io, sil.org, wiki.com, tistory.com등은 해제하였습니다.
- 사용하는 편집기는 CKeditor입니다. 편집기에서 [enter]를 누르면 <p> 태그가 들어가고, 문단으로 생각하고 한줄을 비웁니다. 글줄만 바꾸려면 shift-enter 를 누르시면 <BR>가 들어가므로 용도에 맞게 나누어 쓸 수 있습니다.
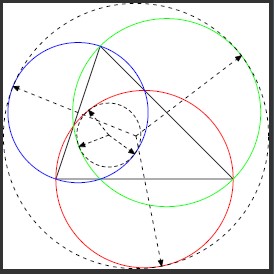
유투브 Michael Penn 콘텐츠를 보다가 내용의 그림이 정확하게 그려지 있지 않아서 메타포스트를 이용하여 그림을 그렸습니다. 조금 수식정리를 하면 얻을 수 있는 결과인데 혹시 어떤 분들에게 새로운 내용이 될 수도 있을 것 같아서 공유합니다.
*내용* 삼각형의 각 변을 지름으로 세원의 접원 그리기
댓글 7
-
큰바위
2021.05.02 13:28
-
김퍼프
2021.05.02 14:03
.mp파일이 업로드가 않되네요. 컴맹수준이라 여기에 원본 mp파일을 올립니다.
verbatimtex
\input kotexutf.tex
etex;
% In compiling, mpost foo (.mp omitted)
% and mptopdf foo (.mp omitted)
beginfig(1)%---------------둔각삼각형----------- refer to YOUTUBER, Michael Penn
u=10mm;
numeric a[],b[],c[],d[], h, k, r, rr;%center(h, k), radii r, rr;
pair A, B, C;
A=(-2, 0); %wlog, A=(-a, 0), B=(a, 0), C=(b, c)
B=(2, 0);
C=(-2.5, 3); %C=(0, 2*sqrt(3)) eqilateral triangle;
a1=xpart A;
a2=ypart A;
b1=xpart B;
b2=ypart B;
c1=xpart C;
c2=ypart C;
d1=abs(A-B);
d2=abs(B-C);
d3=abs(C-A);
%solve simultaneous eq.
% dist((h, k), mid(A,B))=r-dist(A,B)/2---(1)
% dist((h, k), mid(B,C))=r-dist(B,C)/2---(2)
% dist((h, k), mid(C,A))=r-dist(C,A)/2---(3)
numeric adotb, bdotc, cdota;
adotb=a1*b1+a2*b2;
bdotc=b1*c1+b2*c2;
cdota=c1*a1+c2*a2;
(a1-c1)*h+(a2-c2)*k-(d1-d2)*r=adotb-bdotc;%(1)-(2)
(b1-a1)*h+(b2-a2)*k-(d2-d3)*r=bdotc-cdota;%(2)-(3)
%get h, k in terms of r and substitute these to one of (1), (2), (3),
%and we have the quadratic eq.(*) with respect to radius r
numeric t[], s[];%temporary variables
t1=((d1-d2)*(b2-a2)-(d2-d3)*(a2-c2))/((a1-c1)*(b2-a2)-(b1-a1)*(a2-c2));
s1=((adotb-bdotc)*(b2-a2)-(bdotc-cdota)*(a2-c2))/((a1-c1)*(b2-a2)-(b1-a1)*(a2-c2));
t2=((d1-d2)*(b1-a1)-(d2-d3)*(a1-c1))/((a2-c2)*(b1-a1)-(b2-a2)*(a1-c1));
s2=((adotb-bdotc)*(b1-a1)-(bdotc-cdota)*(a1-c1))/((a2-c2)*(b1-a1)-(b2-a2)*(a1-c1));
numeric l, m, n;%coefficients of quadratic eq. l*r*r + m*r + n = 0 ---- (*)
l=t1*t1+t2*t2-1;
m=2*t1*s1+2*t2*s2-(a1+b1)*t1-(a2+b2)*t2+d1;
n=s1*s1+s2*s2-(a1+b1)*s1-(a2+b2)*s2+adotb;
r=(0-m+sqrt(m*m-4*l*n))/(2*l);%roots of quadratic eq.(*)
rr=(0-m-sqrt(m*m-4*l*n))/(2*l);
draw (A--B--C--cycle) scaled u;%---input triangle & circles
draw (fullcircle scaled d1 shifted 0.5[A,B]) scaled u withcolor red;
draw (fullcircle scaled d2 shifted 0.5[B,C]) scaled u withcolor green;
draw (fullcircle scaled d3 shifted 0.5[C,A]) scaled u withcolor blue;
h:=t1*rr+s1;
k:=t2*rr+s2;
draw (fullcircle scaled (2*rr) shifted (h,k)) scaled u dashed dashpattern(on 2bp off 3bp);%---results
pair P,Q,R;%tangent points
P:=(rr/(rr-0.5*d1))[(h,k), 0.5[A,B]];
Q:=(rr/(rr-0.5*d2))[(h,k), 0.5[B,C]];
R:=(rr/(rr-0.5*d3))[(h,k), 0.5[C,A]];
for i=P, Q, R: drawarrow ((h,k)--i) scaled u dashed dashpattern(on 2bp off 3bp); endfor;
h:=t1*r+s1;
k:=t2*r+s2;
draw (fullcircle scaled (2*r) shifted (h,k)) scaled u dashed dashpattern(on 2bp off 2bp);%---results
P:=(r/(r-0.5*d1))[(h,k), 0.5[A,B]];
Q:=(r/(r-0.5*d2))[(h,k), 0.5[B,C]];
R:=(r/(r-0.5*d3))[(h,k), 0.5[C,A]];
for i=P, Q, R: drawarrow ((h,k)--i) scaled u dashed dashpattern(on 2bp off 2bp); endfor;
endfig;
beginfig(2)%직각삼각형
numeric a[],b[],c[],d[], h, k, r, rr;%center(h, k), radii r, rr;
pair A, B, C;
A=(-2, 0); %wlog, A=(-a, 0), B=(a, 0), C=(b, c)
B=(2, 0);
C=(-2, 3);
a1=xpart A;
a2=ypart A;
b1=xpart B;
b2=ypart B;
c1=xpart C;
c2=ypart C;
d1=abs(A-B);
d2=abs(B-C);
d3=abs(C-A);
%solve simultaneous eq.
% dist((h, k), mid(A,B))=r-dist(A,B)/2---(1)
% dist((h, k), mid(B,C))=r-dist(B,C)/2---(2)
% dist((h, k), mid(C,A))=r-dist(C,A)/2---(3)
numeric adotb, bdotc, cdota;
adotb=a1*b1+a2*b2;
bdotc=b1*c1+b2*c2;
cdota=c1*a1+c2*a2;
(a1-c1)*h+(a2-c2)*k-(d1-d2)*r=adotb-bdotc;%(1)-(2)
(b1-a1)*h+(b2-a2)*k-(d2-d3)*r=bdotc-cdota;%(2)-(3)
%get h, k in terms of r and substitute these to one of (1), (2), (3),
%and we have the quadratic eq.(*) with respect to radius r
numeric t[], s[];%temporary variables
t1=((d1-d2)*(b2-a2)-(d2-d3)*(a2-c2))/((a1-c1)*(b2-a2)-(b1-a1)*(a2-c2));
s1=((adotb-bdotc)*(b2-a2)-(bdotc-cdota)*(a2-c2))/((a1-c1)*(b2-a2)-(b1-a1)*(a2-c2));
t2=((d1-d2)*(b1-a1)-(d2-d3)*(a1-c1))/((a2-c2)*(b1-a1)-(b2-a2)*(a1-c1));
s2=((adotb-bdotc)*(b1-a1)-(bdotc-cdota)*(a1-c1))/((a2-c2)*(b1-a1)-(b2-a2)*(a1-c1));
numeric l, m, n;%coefficients of quadratic eq. l*r*r + m*r + n = 0 ---- (*)
l=t1*t1+t2*t2-1;
m=2*t1*s1+2*t2*s2-(a1+b1)*t1-(a2+b2)*t2+d1;
n=s1*s1+s2*s2-(a1+b1)*s1-(a2+b2)*s2+adotb;
r=(0-m+sqrt(m*m-4*l*n))/(2*l);%roots of quadratic eq.(*)
rr=(0-m-sqrt(m*m-4*l*n))/(2*l);
draw (A--B--C--cycle) scaled u;%---input triangle & circles
draw (fullcircle scaled d1 shifted 0.5[A,B]) scaled u withcolor red;
draw (fullcircle scaled d2 shifted 0.5[B,C]) scaled u withcolor green;
draw (fullcircle scaled d3 shifted 0.5[C,A]) scaled u withcolor blue;
h:=t1*rr+s1;
k:=t2*rr+s2;
draw (fullcircle scaled (2*rr) shifted (h,k)) scaled u dashed dashpattern(on 2bp off 3bp);%---results
pair P,Q,R;%tangent points
P:=(rr/(rr-0.5*d1))[(h,k), 0.5[A,B]];
Q:=(rr/(rr-0.5*d2))[(h,k), 0.5[B,C]];
R:=(rr/(rr-0.5*d3))[(h,k), 0.5[C,A]];
for i=P, Q, R: drawarrow ((h,k)--i) scaled u dashed dashpattern(on 2bp off 3bp); endfor;
h:=t1*r+s1;
k:=t2*r+s2;
draw (fullcircle scaled (2*r) shifted (h,k)) scaled u dashed dashpattern(on 2bp off 2bp);%---results
P:=(r/(r-0.5*d1))[(h,k), 0.5[A,B]];
Q:=(r/(r-0.5*d2))[(h,k), 0.5[B,C]];
R:=(r/(r-0.5*d3))[(h,k), 0.5[C,A]];
for i=P, Q, R: drawarrow ((h,k)--i) scaled u dashed dashpattern(on 2bp off 2bp); endfor;
endfig;
end
-
Mposter
2021.05.03 08:01
올려주신 소스를 테스트할 수 있게 정리했습니다.
-
큰바위
2021.05.03 14:27
lualatex test.tex을 실행해도 결과를 얻지 못하는 것이 혹시 제게 문제가 있는 것인지 모르겠군요.
무엇인가 전제 되는 것이 혹시 있는 것입니까?
-
yihoze
2021.05.03 15:28
lualatex으로 한 번 컴파일해서 오류 없이 제대로 나오는데요.
-
noname
2021.05.03 17:23
virtualbox에 설치된 linuxmint에서 해봤는데 이상없이 잘 됩니다. texlive는 2019-20200218인가입니다.
sudo apt install texlive-luatex texlive-metapost
이걸로 되던데요.
-
큰바위
2021.05.03 20:16
아이고 역시. 열심히 metapost를 검색하고 메뉴얼도 읽어 봤는데, 설치에 대한 언급이 없어서 설치을 안하고 정말 무대포로 실행했군요. 현재 tex--version은 2020-202102입니다. metapost 설치하니 잘 됩니다. 감사.
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 978 |
애니메이션
[2] | yihoze | 2021.11.24 | 670 |
| 977 |
두 이미지들을 모두 또는 선택적으로 삽입하기
[2] | yihoze | 2021.11.23 | 700 |
| 976 | TinyTeX 간단 리뷰 [5] | noname | 2021.11.05 | 1066 |
| 975 |
문화부 글꼴에 관하여
[2] | noname | 2021.10.29 | 980 |
| 974 | Spix 소개 [5] | noname | 2020.07.27 | 4015 |
| 973 | kswrapfig 수정본, 발표자료 [4] | nova de hi | 2012.02.06 | 24787 |
| 972 |
은 글꼴 폰트 세팅
[2] | noname | 2020.06.08 | 3846 |
| 971 |
안중근 의거일, <동양평화론> 서문
[1] | noname | 2021.10.26 | 799 |
| 970 |
한자에 독음을 다는 몇 가지 방법
[10] | nanim | 2015.04.29 | 5926 |
| 969 |
정본 훈민정음 언해 어제 서문
[9] | noname | 2021.09.17 | 1406 |
| 968 | 한글날이네요 [10] | Progress | 2021.10.09 | 1061 |
| 967 | 정본 <훈민정음 언해> 2 [7] | noname | 2021.09.27 | 1171 |
| 966 |
스타일 매크로
[4] | yihoze | 2021.09.15 | 1149 |
| 965 |
네이버 마루부리 폰트 테스트
[4] | Progress | 2021.10.06 | 1290 |
| 964 |
철 지난 맥 OS에 텍라이브 2021 설치하기
[5] | Progress | 2021.05.02 | 3144 |
| 963 |
xetexko의 한자음
| noname | 2021.09.25 | 948 |
| 962 |
ichingforyou 2021
[6] | noname | 2021.09.11 | 1142 |
| 961 | 우리말을 찾아 주시길. [2] | 큰바위 | 2021.09.12 | 1110 |
| 960 | tabularray 패키지 예찬 [9] | yihoze | 2021.08.31 | 1422 |
| 959 | 가입 인사 드려요 | 김선호 | 2021.08.11 | 1336 |


올려주신 5개의 그림 가운데 적어도 하나, 세모들과 동그라미를 어떻게 metapost로 짰는지 보여주셔야
솔깃하지 않을까요?